Introduction

Preparing for the Probability (P) Exam? Here’s What You Need to Know!

The Probability (P) Exam, administered by the Society of Actuaries (SOA), is a critical step in your actuarial journey. This 3-hour computer-based test consists of 30 multiple-choice questions, assessing your understanding of probability concepts essential for risk assessment.

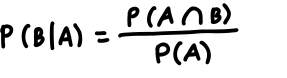
Exam Details:

✅ Basic calculus knowledge required.
✅ Valid passport needed for exam day.
✅ Recommended calculator: TI-30XS.
✅ Exam fee: ~$135 USD for candidates in India.
✅ Offered in: January, March, May, July, September, and November.
✅ Registration closes: ~one month before the exam date.
✅ Results: Preliminary pass/fail immediately; official results within 8-11 weeks.
✅ Suggested study time: ~300 hours for thorough preparation.

Core Exam Topics:

✔️ General Probability – Fundamental probability rules & theorems.
✔️ Univariate Probability Distributions – Single-variable probability distributions.
✔️ Multivariate Probability Distributions – Joint distributions & multiple variables.
✔️ Insurance & Risk Management – Applying probability in risk assessment.

Next Steps After Exam P:

Once you pass, you can move on to the Financial Mathematics (FM) Exam or, if FM is already completed, proceed to Fundamentals of Actuarial Mathematics (FAM) or Statistics for Risk Modeling (SRM).

The Probability (P) Exam is a challenging yet rewarding milestone. With the right preparation, you can set yourself up for success in your actuarial career!